Movimento harmónico simples: sua correspondência com o movimento circular uniforme

OBJETIVO DA EXPERIÊNCIA

Esta experiência está dirigida aos alunos de 12º ano de escolaridade. Comprovaremos a correspondência que existe entre o movimento harmónico simples e o movimento circular.

Obteremos a cinemática de um sistema de movimento harmónico simples, mediante a associação a um movimento circular uniforme.

MATERIAIS NECESSÁRIOS

• Fita adesiva
• Fita de papel
• Cabo de ligação 1.000 Vermelho (2)
• Cone de roldanas
• Crono vibrador
• Desaparafusador
• Disco suporte
• Eixo tambor
• Fonte de alimentação
• Gancho (2)
• Fio de nylon de 0,4
• Jogo de pesos:
  • Peso de 2,5 g
  • Peso de 10 g
  • Peso de 50 g
  • Peso de 100 g
  • Peso de 200 g
• Junta tórica
• Motor com redutor
• Noz dupla (5)
• Papel milimétrico
• Roldana com haste (2)
• Portapesos
• Parafuso de arraste
• Parafuso de mesa (2)
• Triplo decímetro
• Vareta eixo
• Vareta suporte (2)

FUNDAMENTOS TEÓRICOS

O movimento circular é o exemplo mais simples do movimento periódico.

Imaginemos uma bola que percorre uma circunferência, percorrerá a mesma trajetória e repete a sua passagem pela mesma posição, com a mesma velocidade e a mesma aceleração cada certo tempo T que chamaremos período.

O movimento harmónico simples é o que leva um carro que se desloca sobre uma linha reta uma mesma distância ao redor da sua posição de equilíbrio com uma aceleração que é, em todo o momento, proporcional e de sentido contrário ao alongamento.

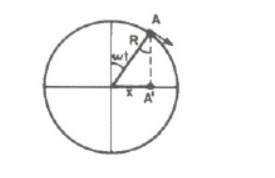
O movimento harmónico e o circular uniforme, estão relacionados entre si: quando um ponto A percorre uma circunferência com velocidade angular constante 0, a sua projeção A' sobre un diâmetro move-se com movimento harmónico simples.

O alongamento de A' será:

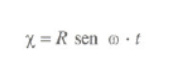
O movimento harmónico é um dos mais frequentes na Física.

INSTRUÇÕES PARA REALIZAR A EXPERIÊNCIA

Vamos montar o dispositivo experimental da figura seguinte. Para isso seguiremos o video da experiência que está no final do artigo::

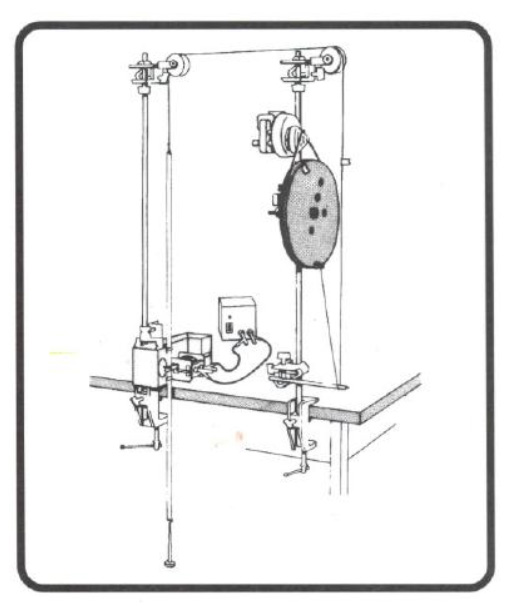
Atamos o fio, com um nó folgado, ao parafuso da beira do disco de suporte. No ponto diametralmente oposto ao parafuso, colamos uma pedaço de fita adesiva, que servirá como ponto de referência do movimento circular. Fazemos girar o disco até que essa marca esteja na parte superior.

Colamos outra pedaço de fita adesiva sobre o fio vertical de modo que fique à mesma altura da anterior.

Pomos o motor em marcha e observamos que ambas as marcas se movem sincronizadas. A do disco efetua un movimento circular, enquanto q do fio descreve um movimento vertical alternativo sendo, em todo o momento, a projeção da outra sobre o diâmetro: dá-se um movimento harmónico.

Observamos que o porta pesos também segue um movimento harmónico. Quando esteja na sua posição mais baixa, ligamos o crono vibrador e o desligamos quando chegar à sua posição superior.

CÁLCULOS E RESULTADOS

Colamos a fita obtida numa folha de papel milimétrico. Medimos a distância que há entre os pontos extremos e traçamos uma semicircunferência que tenha por diâmetro essa distância.

Como o número de pontos obtidos na fita é excessivo, para simplificar os cálculos somente se considerariam significativos um em cada 10 pontos.

Tomamos como referência o ponto mais próximo ao centro da fita e a partir desse, assinalamos as marcas de 10 em 10.

Se os pontos extremos estiverem tão próximos entre si que não se podem distinguir, pode prescindir-se deles.

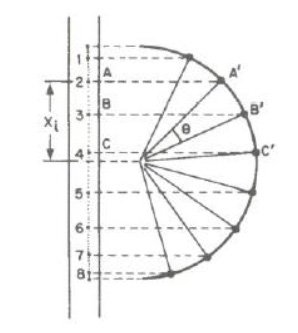
Numeramos correlativamente os pontos significativos a partir de um extremo. Para cada um destes pontos traçam-se perpendiculares na fita, que cortarão a semicircunferência nos pontos A', B',...

Comprovamos que os arcos A 'B', B'C', C'D', são sensivelmente iguais entre si, embora os segmentos AB, BC, CD, não o sejam.

Traçamos os raios 0A', 0B', 0C’,...e medimos os ângulos θ1, θ2, θ3, … de cada setor formado. Comprovamos que são praticamente iguais. Isto demonstra a relação que existe entre o movimento harmónico e o circular uniforme.

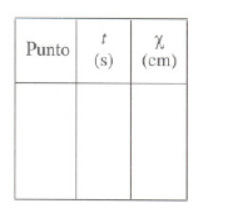
Medimos las distâncias (alongamentos) de cada ponto significativo no centro da fita, começando pelo que está situado num extremo e criamos uma tabela de valores como a siguente:

Recordamos que o tempo que decorre entre duas marcas consecutivas da fita é de 0,02 segundos. Por conseguinte, o tempo que separa dois pontos significativos é de

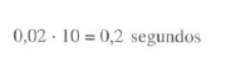
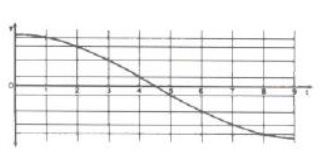
Em papel milimétrico representamos o gráfico de alongamento X em função do tempo t. Ao unir os pontos obteremos uma linha sinusoidal.

Tomar em atenção que o movimento não é perfeitamente harmónico simples, já que o fio que se segura no disco não segue um movimento vertical.

VIDEO DA EXPERIÊNCIA