Como medir a velocidade do som

ou seja

OBJETIVO DA EXPERIÊNCIA

Com esta atividade tentaremos calcular a velocidade do som utilizando um tubo ressonador cuja frequência própria seja a mesma que a do diapasão.

MATERIAIS NECESSÁRIOS

• Diapasão de 440 Hz
• Martelo para diapasão
• Noz dupla
• Pinças para bureta
• Proveta graduada de 100 cm3
• Rolha
• Parafuso  de mesa
• Triplo decímetro
• Tubo de borracha
• Tubo de vidro de 25Ømm x 250mm
• Vareta suporte

FUNDAMENTOS TEÓRICOS

Ao vibrar um diapasão junto à boca de um tubo, fechado na outra extremidade, as compressões e dilatações propagam-se através do ar no tubo e chegam ao fundo, desde onde voltam refletidos.

As ondas diretas com as que voltam, dão lugar a ondas estacionárias, capas ventrais, onde o ar vibra com máxima amplitude, e capas de nós, onde não se move.

Na extremidade fechada do tubo, formar-se-á um nó uma vez que a última capa de ar, em contacto com o fundo não pode vibrar. Além disso, para que o som seja audível, é condição necessária que na boca do tubo se forme um ventre.

Estas condições nos limites somente podem dar-se quando os nós e os ventres intermédios dividem o tubo em um número impar de partes, sendo cada uma a distância entre ventre e nó consecutivo que, como se sabe, vale 'A'/4. O comprimento total do tubo será um número impar de quartos de onda.

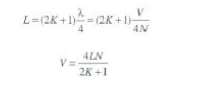
O ar do tubo pode vibrar, pois, de várias formas, representadas no desenho, às quais correspondem diferentes frequências próprias, calculáveis; K =0, 1, 2... com a fórmula anterior.

As ondas estacionárias do ar serão intensas quando a frequência do diapasão que a provoca coincida com alguma destas frequências próprias do tubo, ou seja, quando haja ressonância.

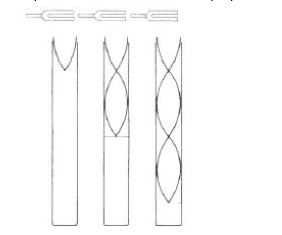
Para o som fundamental K =0 a fórmula fica:

V= 4LN

INSTRUÇÕES PARA REALIZAR A EXPERIÊNCIA

Realizar a montagem da figura 1

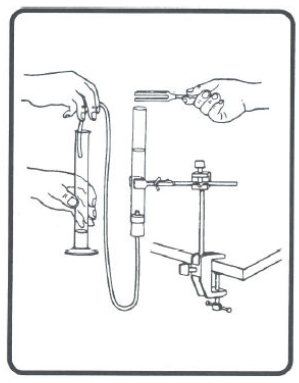
A extremidade livre do tubo de borracha, vai por cima da extremidade aberta do tubo, mantendo-o nessa posição com a  mão.

Nestas condições, encher de água o tubo com a ajuda da proveta graduada, até à borda. Uma vez o tubo cheio, esvaziar a proveta completamente caso ainda tenha alguma água e introduzir a extremidade livre do tubo de borracha na proveta, mas de forma a que em nenhum momento fique abaixo do nível de água no tubo.

Nesta situação, outro operador segura o diapasão de 440 Hz com uma mão e fazendo-o vibrar coloca-o na boca do tubo.

Entretanto, o que segura a proveta, começa a baixá-la lentamente ao mesmo tempo que o nível da água no tubo vai baixando. Se as vibrações do diapasão começarem a diminuir, o encarregado por elas, deverá aumentá-las com o martelo.

Observa-se que há um momento em que som é amplificado, para começar logo a diminuir.

Encher de novo o tubo com água e repetir a experiência. Em três ou quatro ensaios deixa-se o nível, exatamente na posição em que o som é mais forte.  Medir com o triplo decímetro o comprimento L desde a beira do tubo até à superfície de água.

Operando desta forma no pode haver mais que um ventre na boca e um nó junto à água. Na realidade, o ventre forma-se um pouco mais acima e por isso convém corrigir o comprimento L da medição, somando-lhe 0,6R, sendo R o raio do tubo.

CÁLCULOS E RESULTADOS

Com estes dados e aplicando a segunda fórmula pode calcular-se a velocidade do som.

VIDEO DA EXPERIÊNCIA